Unveiling The Power Of Dimensionality Reduction: A Comprehensive Exploration Of UMAP And T-SNE

Unveiling the Power of Dimensionality Reduction: A Comprehensive Exploration of UMAP and t-SNE

Related Articles: Unveiling the Power of Dimensionality Reduction: A Comprehensive Exploration of UMAP and t-SNE

Introduction

With great pleasure, we will explore the intriguing topic related to Unveiling the Power of Dimensionality Reduction: A Comprehensive Exploration of UMAP and t-SNE. Let’s weave interesting information and offer fresh perspectives to the readers.

Unveiling the Power of Dimensionality Reduction: A Comprehensive Exploration of UMAP and t-SNE

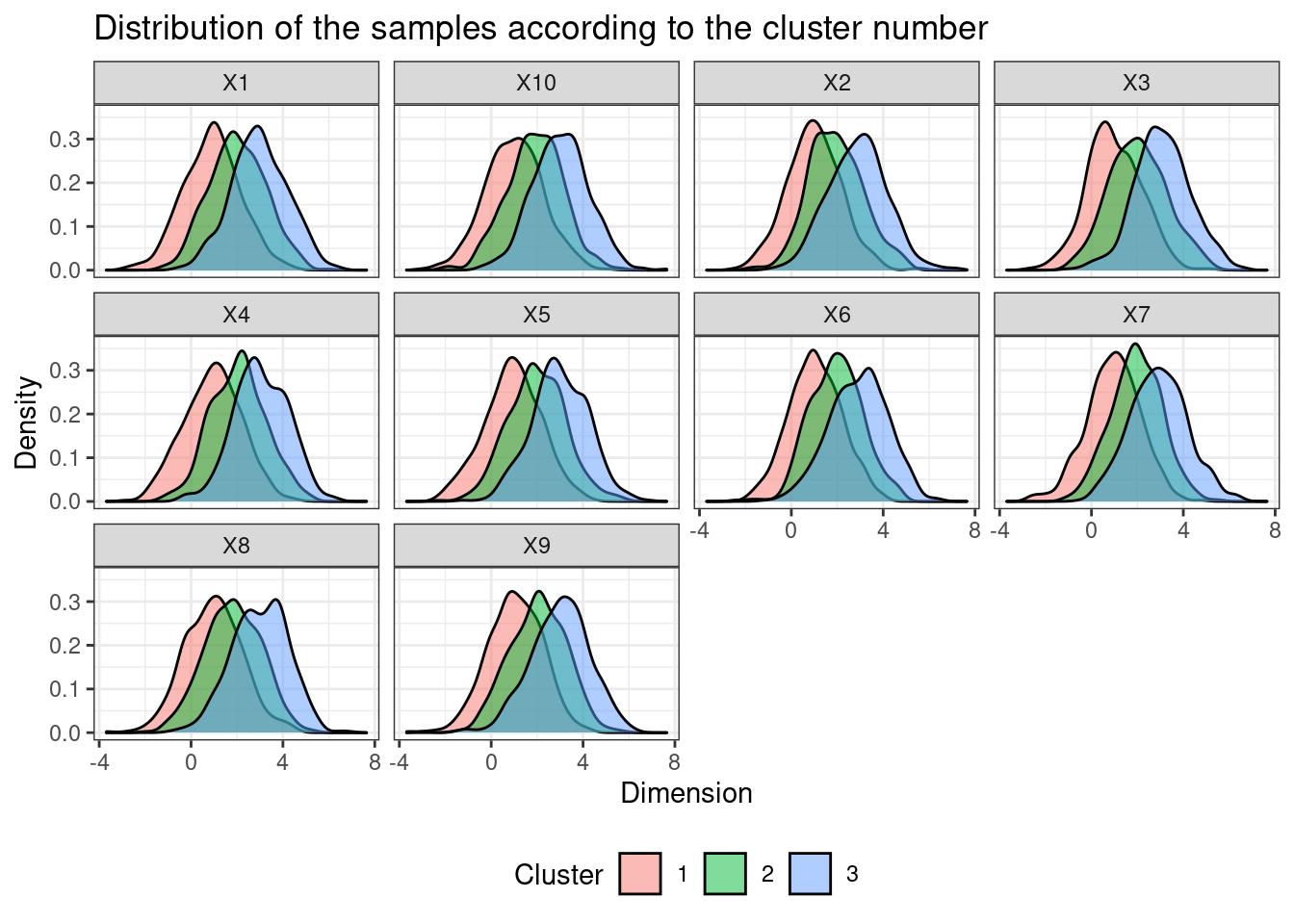
In the realm of data analysis, navigating the complexities of high-dimensional datasets often poses a significant challenge. Visualizing and extracting meaningful insights from such data becomes an arduous task. To address this, dimensionality reduction techniques have emerged as powerful tools, enabling researchers and analysts to glean valuable information from high-dimensional data by transforming it into a lower-dimensional representation. Among these techniques, two prominent methods stand out: Uniform Manifold Approximation and Projection (UMAP) and t-Distributed Stochastic Neighbor Embedding (t-SNE).

UMAP: A Topological Approach to Dimensionality Reduction

UMAP is a relatively new but rapidly gaining popularity among data scientists. It stands out for its ability to preserve the global structure of the data, capturing both local and global relationships between data points. This is achieved through a novel approach that leverages topological data analysis, specifically the notion of a manifold.

Understanding the Manifold Concept: Imagine a crumpled piece of paper. While the paper itself is two-dimensional, the crumpled form appears three-dimensional. This crumpled form represents a manifold, a geometric object that can be locally approximated by a Euclidean space. Data points in high-dimensional spaces often lie on such manifolds, and UMAP seeks to uncover these underlying structures.

Key Features of UMAP:

• Topological Data Analysis: UMAP incorporates topological data analysis, which focuses on the shape and structure of the data, rather than just the distances between points. This allows it to capture more complex relationships and retain the global structure of the data.
• Non-linearity: UMAP is inherently non-linear, meaning it can handle data with complex relationships that cannot be captured by linear methods.
• Scalability: Unlike t-SNE, UMAP is more scalable, making it suitable for handling large datasets.
• Parameter Tuning: UMAP offers a relatively small number of parameters to tune, simplifying the process of finding optimal settings for a given dataset.

Applications of UMAP:

• Data Visualization: UMAP excels at visualizing complex high-dimensional data, enabling researchers to gain insights into the underlying structure and patterns within the data.
• Clustering and Classification: UMAP can be used to cluster data points into meaningful groups, facilitating further analysis and classification tasks.
• Anomaly Detection: By identifying outliers and deviations from the manifold structure, UMAP can aid in detecting anomalies within the data.

t-SNE: A Probabilistic Approach to Dimensionality Reduction

t-SNE is a widely used and well-established technique for dimensionality reduction. It relies on a probabilistic approach, focusing on preserving local neighborhood relationships between data points. The core idea is to represent high-dimensional data points as points in a lower-dimensional space, while maintaining the relative distances between nearby points.

Key Features of t-SNE:

• Probabilistic Approach: t-SNE uses a probabilistic framework to model the relationships between data points, focusing on preserving local neighborhoods.
• Non-linearity: Similar to UMAP, t-SNE is non-linear, capable of capturing complex relationships in the data.
• Visualization: t-SNE is particularly effective at visualizing high-dimensional data, revealing clusters and patterns that may not be apparent in the original space.
• Parameter Sensitivity: t-SNE is known to be sensitive to parameter settings, requiring careful tuning to achieve optimal results.

Applications of t-SNE:

• Data Visualization: t-SNE excels at visualizing high-dimensional data, particularly for exploratory analysis and understanding the underlying structure of the data.
• Clustering and Classification: t-SNE can be used to cluster data points and identify distinct groups within the data, aiding in classification tasks.
• Anomaly Detection: t-SNE can reveal outliers and deviations from the typical distribution of data points, facilitating anomaly detection.

Comparing UMAP and t-SNE: Choosing the Right Tool

While both UMAP and t-SNE are powerful dimensionality reduction techniques, they differ in their strengths and weaknesses. The choice between the two ultimately depends on the specific requirements of the analysis.

UMAP:

• Strengths: Preserves global structure, scalable, fewer parameters to tune.
• Weaknesses: Can struggle with highly non-linear data, may not be as effective for visualizing extremely high-dimensional data.

t-SNE:

• Strengths: Excellent for visualizing complex data, effective for revealing subtle clusters and patterns.
• Weaknesses: Sensitive to parameter settings, less scalable than UMAP, may not preserve global structure as well.

Choosing the Right Approach:

• For visualizing large datasets with complex relationships and preserving global structure: UMAP is a better choice.
• For visualizing high-dimensional data with a focus on local neighborhoods and revealing subtle clusters: t-SNE is a suitable option.
• For highly non-linear data: UMAP may be more appropriate, but careful parameter tuning is essential for both methods.

Beyond Visualization: Exploring the Applications of UMAP and t-SNE

Beyond visualization, UMAP and t-SNE find applications in various fields, including:

• Machine Learning: Both techniques can be used to reduce the dimensionality of features in machine learning models, improving performance and reducing computational costs.
• Natural Language Processing: UMAP and t-SNE can be applied to reduce the dimensionality of word embeddings, facilitating text classification and topic modeling.
• Bioinformatics: These techniques are used in analyzing gene expression data, uncovering relationships between genes and identifying disease subtypes.
• Image Processing: UMAP and t-SNE can be applied to reduce the dimensionality of image features, enabling image classification and object recognition.

FAQ: Addressing Common Queries about UMAP and t-SNE

1. What is the difference between UMAP and t-SNE?

UMAP and t-SNE are both dimensionality reduction techniques, but they differ in their underlying principles and strengths. UMAP focuses on preserving the global structure of the data using topological data analysis, while t-SNE emphasizes preserving local neighborhoods through a probabilistic approach.

2. When should I use UMAP?

UMAP is suitable for visualizing large datasets with complex relationships, preserving the global structure of the data. It is also a good choice when scalability is a concern.

3. When should I use t-SNE?

t-SNE is best suited for visualizing high-dimensional data with a focus on local neighborhoods and revealing subtle clusters. It is particularly useful for exploratory analysis and uncovering hidden patterns.

4. How do I choose the right parameters for UMAP and t-SNE?

Both techniques require careful parameter tuning to achieve optimal results. The optimal parameters vary depending on the specific dataset and the desired outcome. Experimentation and visualization are crucial for finding the best settings.

5. Can I use UMAP or t-SNE for classification tasks?

Yes, both techniques can be used for classification tasks. By reducing the dimensionality of the data, they can simplify the classification process and improve the performance of machine learning models.

Tips for Utilizing UMAP and t-SNE Effectively

• Data Preprocessing: Ensure your data is properly preprocessed before applying UMAP or t-SNE. This includes scaling the features, handling missing values, and removing outliers.
• Parameter Tuning: Experiment with different parameter settings to find the best configuration for your specific dataset. Visualization is crucial for assessing the results and identifying the optimal parameters.
• Visualization: Utilize visualization tools to gain insights from the reduced-dimensional representation of your data. This will help you understand the underlying structure, identify clusters, and reveal hidden patterns.
• Interpretation: Remember that the reduced-dimensional representation is just a projection of the original data. Interpret the results carefully, considering the limitations of the technique and the context of the data.

Conclusion: Embracing the Power of Dimensionality Reduction

UMAP and t-SNE have revolutionized data analysis by providing powerful tools for understanding and visualizing high-dimensional datasets. By leveraging different approaches, these techniques capture the essence of complex data, revealing hidden patterns and insights. Choosing the right tool depends on the specific analysis requirements, but both UMAP and t-SNE offer invaluable capabilities for exploring and extracting knowledge from complex datasets. As data science continues to evolve, these techniques will undoubtedly play a crucial role in unlocking the secrets hidden within high-dimensional data.

Closure

Thus, we hope this article has provided valuable insights into Unveiling the Power of Dimensionality Reduction: A Comprehensive Exploration of UMAP and t-SNE. We appreciate your attention to our article. See you in our next article!