Unveiling Hidden Structures: A Comprehensive Guide To UMAP Analysis

Unveiling Hidden Structures: A Comprehensive Guide to UMAP Analysis

Related Articles: Unveiling Hidden Structures: A Comprehensive Guide to UMAP Analysis

Introduction

In this auspicious occasion, we are delighted to delve into the intriguing topic related to Unveiling Hidden Structures: A Comprehensive Guide to UMAP Analysis. Let’s weave interesting information and offer fresh perspectives to the readers.

Unveiling Hidden Structures: A Comprehensive Guide to UMAP Analysis

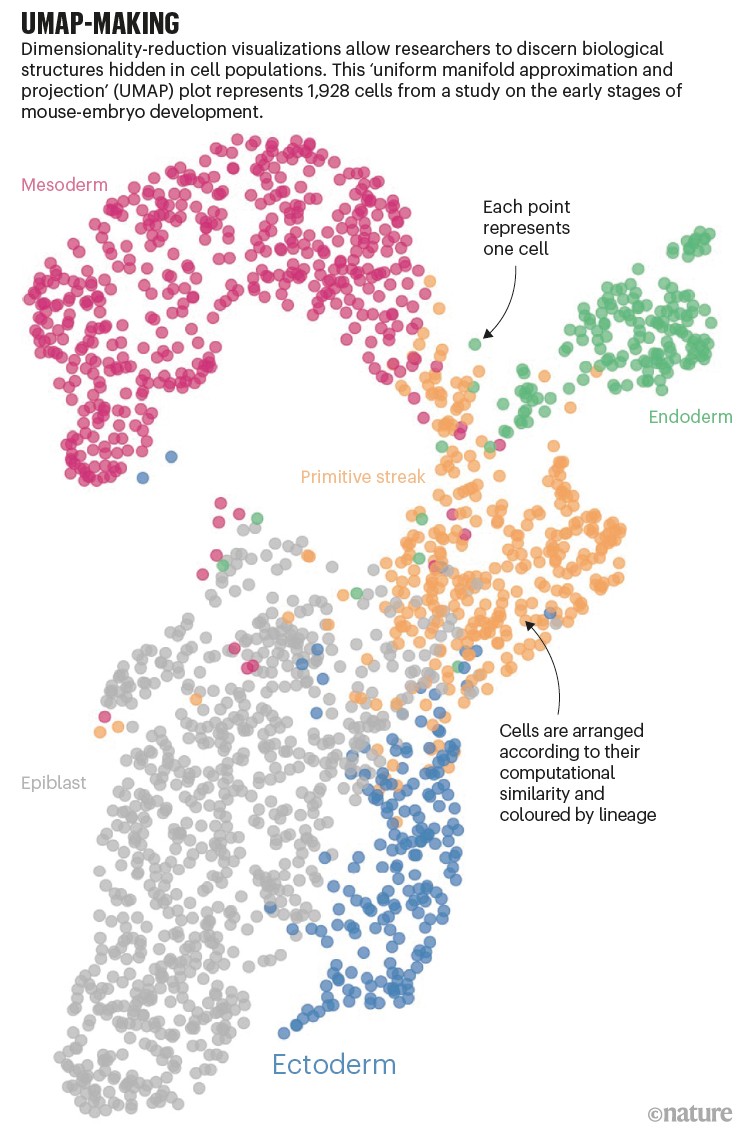
The exploration of complex datasets is a fundamental endeavor in numerous fields, ranging from biology and medicine to finance and social sciences. These datasets often contain intricate relationships and hidden patterns that traditional methods struggle to decipher. Enter Uniform Manifold Approximation and Projection (UMAP), a powerful dimensionality reduction technique that excels in revealing the underlying structure of high-dimensional data. This guide delves into the intricacies of UMAP, explaining its workings, highlighting its benefits, and exploring its diverse applications.

The Challenge of High-Dimensional Data

Imagine navigating a vast, multi-dimensional space. Each dimension represents a different variable, and each data point is a unique location within this space. This is the reality of high-dimensional data, where the number of variables far exceeds the human capacity for visualization and comprehension.

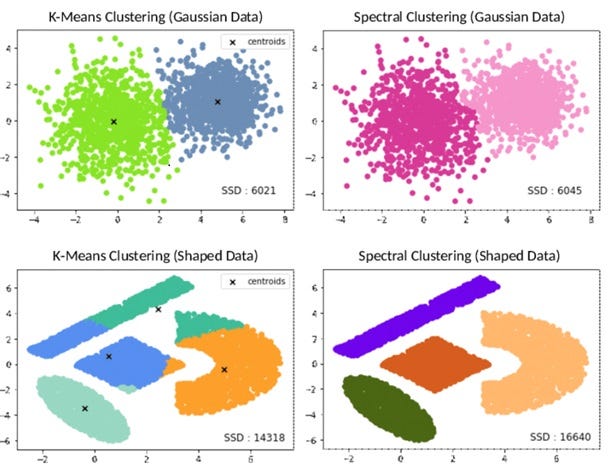
Traditional methods like Principal Component Analysis (PCA) aim to reduce dimensionality by finding the directions of greatest variance in the data. However, PCA struggles with non-linear relationships and can distort the underlying structure of the data, leading to inaccurate insights.

UMAP: Unraveling Non-Linearity

UMAP addresses these limitations by leveraging the concept of manifold learning. A manifold is a continuous, smooth surface embedded within a higher-dimensional space. UMAP assumes that high-dimensional data points lie on a lower-dimensional manifold, meaning that their true relationships can be captured in a lower-dimensional representation.

The algorithm operates in two key stages:

1. Neighborhood Construction: UMAP first identifies the local neighborhood of each data point, capturing its relationships with nearby points. This is achieved by constructing a weighted k-nearest neighbor graph, where edges represent the similarity between points.
2. Global Embedding: UMAP then maps the data points from the high-dimensional space onto a lower-dimensional space, preserving the local neighborhood structure. This projection aims to maintain the distances and relationships between points, ensuring that the resulting representation accurately reflects the underlying manifold.

Key Advantages of UMAP

UMAP offers several advantages over traditional dimensionality reduction techniques:

• Non-linearity: UMAP effectively captures non-linear relationships in the data, allowing for the identification of complex structures that PCA may miss.
• Preservation of Local Structure: The algorithm prioritizes the preservation of local neighborhoods, ensuring that nearby points remain close in the lower-dimensional representation.
• Scalability: UMAP can handle large datasets efficiently, making it suitable for real-world applications.
• Interpretability: The resulting visualizations are often more intuitive and easier to interpret than those generated by other methods.

Applications of UMAP

UMAP’s versatility has led to its widespread adoption in diverse fields:

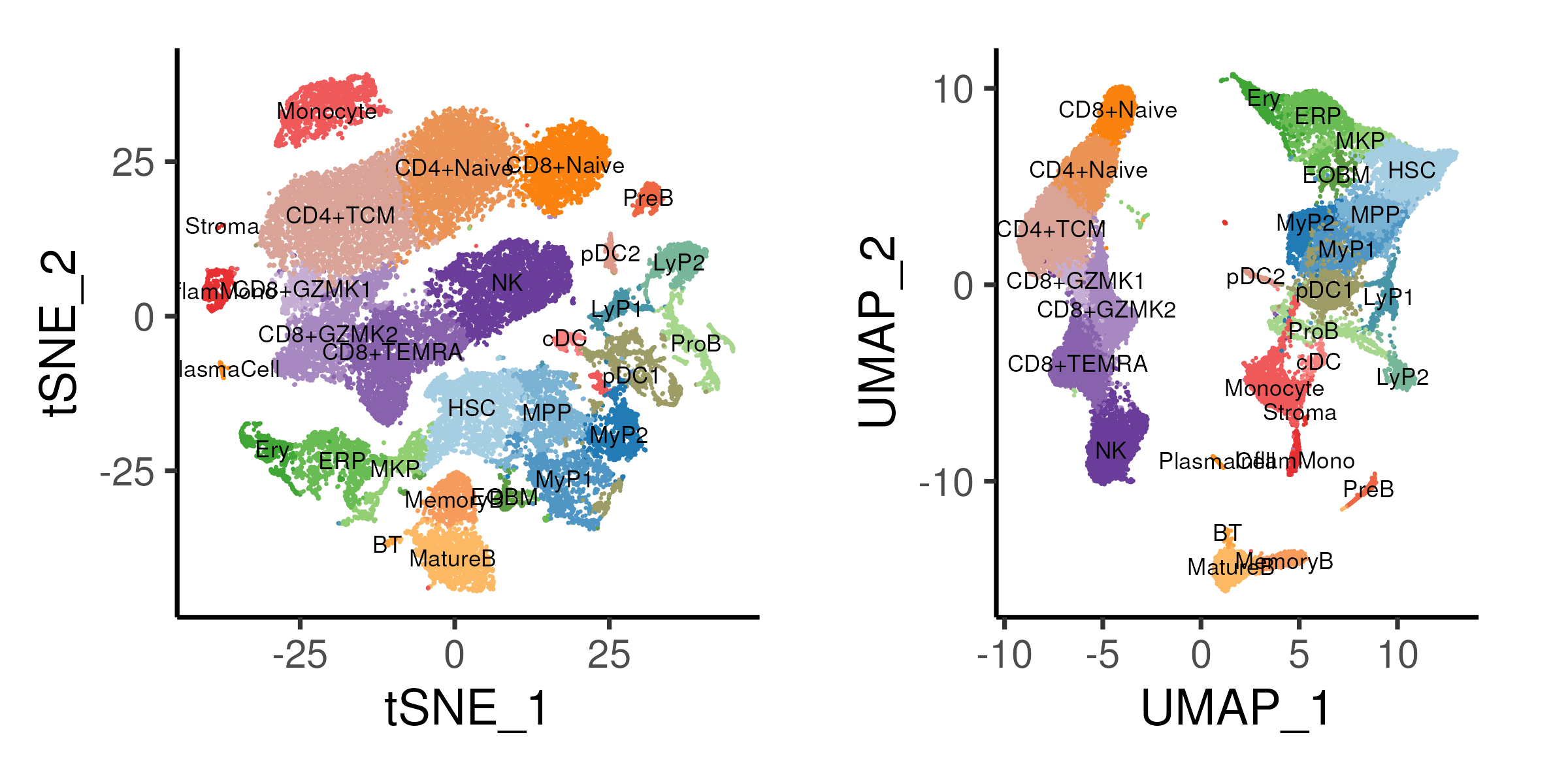
• Data Visualization: UMAP enables the visualization of high-dimensional data, revealing hidden patterns and clusters that might not be apparent in the original space. This is particularly useful in exploratory data analysis and for gaining initial insights into the data’s structure.
• Clustering: UMAP can be used to identify clusters of similar data points, facilitating the discovery of underlying subgroups within a dataset. This is valuable in applications like customer segmentation, disease classification, and anomaly detection.
• Machine Learning: UMAP can be incorporated as a preprocessing step in machine learning tasks, reducing the dimensionality of the input data and potentially improving model performance. This is especially beneficial for algorithms that struggle with high-dimensional inputs.
• Biomedical Research: UMAP has proven valuable in analyzing gene expression data, identifying cell types, and understanding disease progression.
• Social Sciences: UMAP has been employed to analyze social networks, identify communities, and understand the dynamics of information diffusion.

FAQs Regarding UMAP Analysis

Q: What are the limitations of UMAP?

A: While UMAP offers significant advantages, it also has certain limitations:

• Parameter Selection: The performance of UMAP can be sensitive to the choice of parameters, such as the number of neighbors and the embedding dimension. Careful tuning is often required to achieve optimal results.
• Interpretability: While UMAP often produces more interpretable visualizations than other methods, understanding the meaning of the projected dimensions can still be challenging.
• Global Structure: UMAP primarily focuses on preserving local structure, which can sometimes lead to distortions in the global relationships between points.

Q: How does UMAP compare to other dimensionality reduction techniques?

A: UMAP offers several advantages over traditional techniques like PCA:

• Non-linearity: UMAP excels at capturing non-linear relationships, while PCA is limited to linear relationships.
• Local Structure: UMAP prioritizes the preservation of local neighborhoods, while PCA may distort these relationships.
• Scalability: UMAP is generally more scalable than PCA, particularly for large datasets.

Q: How can I implement UMAP in my research?

A: UMAP is readily available in various programming languages and software packages, including Python, R, and MATLAB. Libraries like umap-learn in Python provide a user-friendly interface for implementing UMAP analysis.

Tips for Effective UMAP Analysis

• Data Preprocessing: Ensure that your data is properly preprocessed before applying UMAP. This includes handling missing values, scaling variables, and removing outliers.
• Parameter Tuning: Experiment with different parameter values to optimize the performance of UMAP for your specific dataset.
• Visualization: Utilize effective visualization techniques to explore the results of UMAP analysis and gain insights into the data’s structure.
• Interpretation: Carefully interpret the results of UMAP, considering the context of the data and the chosen parameters.

Conclusion

UMAP stands as a powerful tool for navigating the complexities of high-dimensional data. Its ability to unveil hidden structures, preserve local relationships, and handle large datasets makes it an invaluable asset in various research areas. By leveraging UMAP’s capabilities, researchers can gain deeper insights into their data, uncover previously hidden patterns, and make more informed decisions. As technology continues to generate increasingly complex datasets, UMAP’s role in unlocking the secrets within will only grow in importance.

Closure

Thus, we hope this article has provided valuable insights into Unveiling Hidden Structures: A Comprehensive Guide to UMAP Analysis. We thank you for taking the time to read this article. See you in our next article!