Unveiling Hidden Patterns: A Deep Dive Into UMAP And T-SNE For Dimensionality Reduction

Unveiling Hidden Patterns: A Deep Dive into UMAP and t-SNE for Dimensionality Reduction

Related Articles: Unveiling Hidden Patterns: A Deep Dive into UMAP and t-SNE for Dimensionality Reduction

Introduction

With great pleasure, we will explore the intriguing topic related to Unveiling Hidden Patterns: A Deep Dive into UMAP and t-SNE for Dimensionality Reduction. Let’s weave interesting information and offer fresh perspectives to the readers.

Unveiling Hidden Patterns: A Deep Dive into UMAP and t-SNE for Dimensionality Reduction

In the realm of data analysis, where datasets often reside in high-dimensional spaces, understanding and visualizing intricate relationships can be a formidable challenge. This is where dimensionality reduction techniques come into play, offering a powerful toolset to distill complex data into lower-dimensional representations, revealing hidden patterns and facilitating meaningful insights. Among these techniques, Uniform Manifold Approximation and Projection (UMAP) and t-Distributed Stochastic Neighbor Embedding (t-SNE) have emerged as prominent players, each possessing unique strengths and characteristics.

Understanding the Essence of Dimensionality Reduction

Imagine a dataset comprising thousands of features, each representing a different attribute of the data points. Visualizing such a dataset in its raw form is nearly impossible, as our human perception is limited to three dimensions. Dimensionality reduction techniques address this challenge by transforming the high-dimensional data into a lower-dimensional space, typically two or three dimensions, while preserving the essential relationships and structures present in the original data.

UMAP: Preserving Global Structure and Local Neighborhoods

UMAP stands as a powerful and versatile dimensionality reduction technique, renowned for its ability to preserve both global and local structure in the data. It operates on the principle of approximating the underlying manifold, a geometric structure that captures the intrinsic relationships between data points. UMAP excels in preserving the neighborhood relationships between data points, ensuring that points close together in the high-dimensional space remain close in the lower-dimensional representation.

Key Features of UMAP:

• Topological Data Analysis: UMAP leverages concepts from topological data analysis, allowing it to capture complex geometric structures and relationships present in the data.
• Neighborhood Preservation: UMAP prioritizes preserving the neighborhood relationships between data points, ensuring that nearby points in the high-dimensional space remain close in the reduced space.
• Scalability: UMAP is designed to handle large datasets efficiently, making it suitable for analyzing massive amounts of data.
• Parameter Flexibility: UMAP offers a range of parameters that can be adjusted to fine-tune the dimensionality reduction process, allowing for customization based on the specific needs of the analysis.

t-SNE: Emphasizing Local Structure and Visualization

t-SNE, another prominent dimensionality reduction technique, focuses primarily on preserving local neighborhood structures in the data. It employs a probabilistic approach, mapping data points from a high-dimensional space to a lower-dimensional space while minimizing the Kullback-Leibler divergence between the probability distributions of the high-dimensional and low-dimensional representations.

Key Features of t-SNE:

• Local Structure Preservation: t-SNE excels in preserving the local neighborhood relationships between data points, ensuring that nearby points in the high-dimensional space remain close in the reduced space.
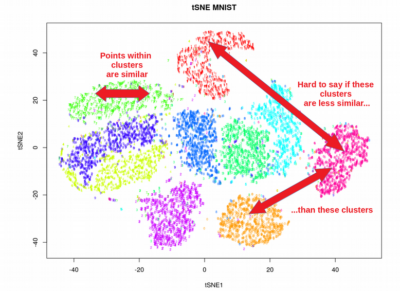
• Visualization Focus: t-SNE is particularly well-suited for visualizing high-dimensional data, enabling the identification of clusters and patterns within the data.
• Sensitivity to Parameters: t-SNE’s performance can be sensitive to the choice of parameters, requiring careful tuning for optimal results.
• Computational Complexity: t-SNE can be computationally intensive, particularly for large datasets, limiting its scalability in certain scenarios.

Choosing Between UMAP and t-SNE: A Comparative Analysis

The choice between UMAP and t-SNE often depends on the specific goals and characteristics of the data analysis task. Here’s a comparative analysis to guide the selection process:

Feature	UMAP	t-SNE
Focus	Global and local structure preservation	Local structure preservation and visualization
Scalability	High	Moderate
Parameter Sensitivity	Moderate	High
Computational Complexity	Moderate	High
Applications	Clustering, anomaly detection, data exploration	Visualization, cluster analysis, data exploration

UMAP is often preferred when preserving both global and local structure is crucial, particularly when dealing with large datasets. Its scalability and flexibility make it suitable for a wide range of data analysis tasks.

t-SNE shines in visualization tasks, particularly when emphasizing local neighborhood relationships and identifying clusters within the data. However, its computational intensity and sensitivity to parameters may limit its use in large-scale datasets or situations requiring high accuracy.

Illustrative Applications of UMAP and t-SNE

The power of UMAP and t-SNE extends across diverse fields, enabling meaningful insights and discoveries:

• Bioinformatics: Analyzing gene expression data, identifying distinct cell types, and understanding disease progression.
• Image Analysis: Clustering images based on visual content, identifying patterns in medical imaging, and classifying objects in satellite imagery.
• Natural Language Processing: Analyzing text data, identifying topics and themes, and understanding sentiment and emotion.
• Machine Learning: Visualizing high-dimensional feature spaces, understanding model behavior, and identifying potential biases.

FAQs: Addressing Common Queries

1. What are the key differences between UMAP and t-SNE?

UMAP emphasizes both global and local structure preservation, while t-SNE primarily focuses on local structure and visualization. UMAP is generally more scalable and less sensitive to parameter choices than t-SNE.

2. When should I use UMAP over t-SNE?

If preserving both global and local structure is crucial, particularly for large datasets, UMAP is a better choice. It offers better scalability and parameter flexibility.

3. When should I use t-SNE over UMAP?

If the primary goal is visualization and emphasizing local neighborhood relationships, particularly for smaller datasets, t-SNE is a suitable option.

4. How do I choose the optimal parameters for UMAP and t-SNE?

Parameter selection depends on the specific dataset and analysis goals. Experimentation and visualization are crucial for finding the optimal settings.

5. Can I use UMAP or t-SNE for high-dimensional data?

Both UMAP and t-SNE are designed to handle high-dimensional data, but their effectiveness may vary depending on the specific dataset and the chosen parameters.

Tips for Effective Use of UMAP and t-SNE

• Data Preprocessing: Ensure data is properly scaled and normalized before applying dimensionality reduction techniques.
• Parameter Tuning: Experiment with different parameters to find the optimal settings for your specific dataset and analysis goals.
• Visualization: Utilize visualization tools to gain insights from the reduced data and validate the effectiveness of the chosen technique.
• Comparison: Compare the results of UMAP and t-SNE to determine the best approach for your specific application.

Conclusion: Unlocking Insights through Dimensionality Reduction

UMAP and t-SNE stand as powerful tools for dimensionality reduction, enabling us to navigate the complexities of high-dimensional data and uncover hidden patterns. While both techniques share a common goal of reducing dimensionality, their strengths and characteristics differ, making them suitable for distinct applications. UMAP excels in preserving both global and local structure, making it ideal for large-scale analysis, while t-SNE prioritizes visualization and local structure, proving valuable for understanding and exploring complex datasets. By leveraging the capabilities of these techniques, we can gain deeper insights into the underlying structures and relationships within our data, paving the way for informed decision-making and groundbreaking discoveries.

Closure

Thus, we hope this article has provided valuable insights into Unveiling Hidden Patterns: A Deep Dive into UMAP and t-SNE for Dimensionality Reduction. We hope you find this article informative and beneficial. See you in our next article!