Navigating The Landscape Of Functional Programming: A Comprehensive Exploration Of Fmap And Applicative Functors

Navigating the Landscape of Functional Programming: A Comprehensive Exploration of fmap and Applicative Functors

Related Articles: Navigating the Landscape of Functional Programming: A Comprehensive Exploration of fmap and Applicative Functors

Introduction

With great pleasure, we will explore the intriguing topic related to Navigating the Landscape of Functional Programming: A Comprehensive Exploration of fmap and Applicative Functors. Let’s weave interesting information and offer fresh perspectives to the readers.

Navigating the Landscape of Functional Programming: A Comprehensive Exploration of fmap and Applicative Functors

The realm of functional programming, characterized by its emphasis on immutability, pure functions, and higher-order functions, presents a unique set of tools for manipulating data and expressing computations. Among these tools, two stand out as particularly crucial: fmap, also known as functor map, and Applicative Functors (AF). These concepts, while seemingly abstract, provide a powerful foundation for writing elegant, concise, and maintainable code, particularly within the context of working with data structures that encapsulate computations or potential values.

Understanding the Essence of Functors

At its core, a functor is a type constructor that enables the application of functions to values within a context. This context can represent various aspects, such as:

• Potential values: Think of a container holding a single value, which might be a result of a computation that hasn’t been performed yet.
• Data structures: Consider a list or a tree, where each element might be subject to a transformation.
• Side effects: Imagine a function that interacts with the outside world, such as writing to a file.

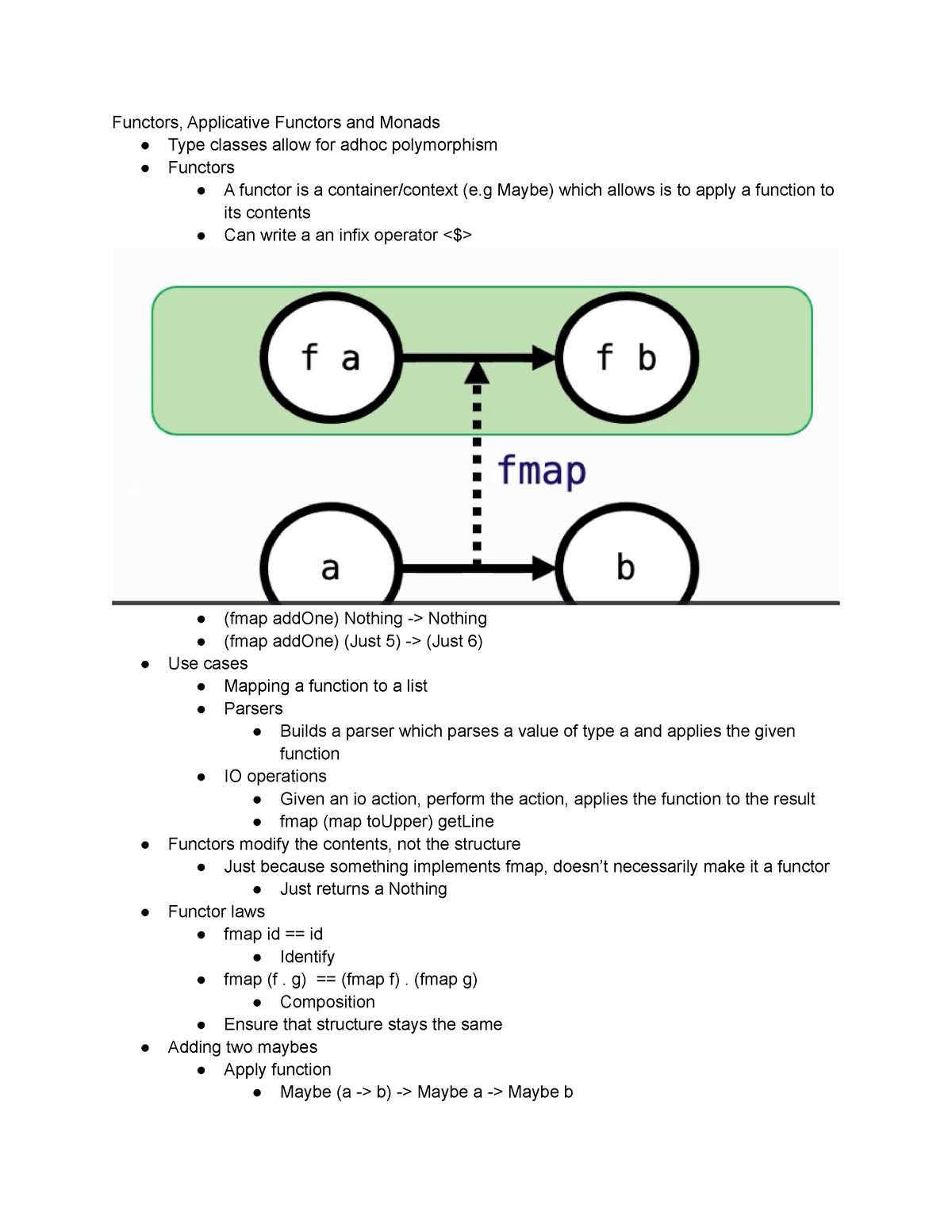
The essence of fmap lies in its ability to apply a function to the value inside a functor without directly accessing that value. This seemingly simple operation unlocks a world of possibilities, allowing for code that is:

• Composed: Multiple transformations can be chained together seamlessly, promoting modularity and reusability.
• Abstract: The specific structure of the functor becomes irrelevant, enabling generic solutions applicable across various contexts.
• Safe: By preserving the context, fmap ensures that the integrity of the underlying data structure is maintained.

Unveiling the Power of Applicative Functors

While fmap allows applying a single function, Applicative Functors extend this capability to multiple functions. They provide a mechanism for applying functions that themselves operate on functors, creating a framework for composing computations within a functorial context.

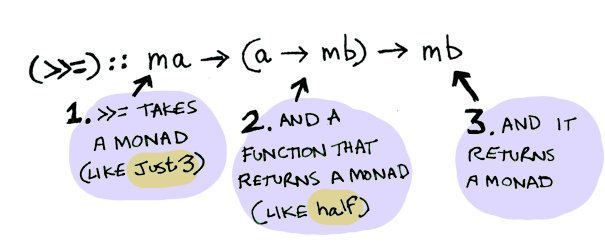
AFs introduce the concept of an applicative function, denoted by the infix operator <*>, which takes two arguments:

• A functor containing a function: This function will be applied to the value within another functor.
• A functor containing a value: This value will be the input to the function.

The applicative function then produces a new functor containing the result of applying the function to the value. This process elegantly encapsulates the application of functions within a context, ensuring that the structure of the functor remains intact.

Illustrative Examples: Bringing fmap and AFs to Life

To truly grasp the power of fmap and AFs, let’s delve into some practical examples:

Example 1: Working with Potential Values (Maybe)

Imagine a function divide that takes two numbers and returns their quotient. However, the second number might be zero, leading to a potential error. We can represent this scenario using the Maybe type, which can hold either a value (Just) or a signal of failure (Nothing):

divide :: Int -> Int -> Maybe Int
divide x 0 = Nothing
divide x y = Just (x / y)

fmap (+1) (Just 5)  -- Output: Just 6
fmap (+1) Nothing  -- Output: Nothing

-- Using Applicative Functor
pure (+1) <*> Just 5  -- Output: Just 6
pure (+1) <*> Nothing  -- Output: Nothing

In this example, fmap applies the function (+1) to the value within the Just constructor, demonstrating its ability to handle potential values gracefully.

Example 2: Transforming Data Structures (Lists)

Consider a list of numbers, and we want to square each element. Using fmap, we can apply the square function to each element without directly accessing the list:

square :: Int -> Int
square x = x * x

fmap square [1, 2, 3]  -- Output: [1, 4, 9]

Example 3: Composing Functions with AFs (IO)

Let’s say we have two functions that perform I/O operations, readFile and writeToFile. We can use AFs to compose these functions, ensuring that the output of readFile is passed to writeToFile:

import System.IO

-- Assuming readFile and writeToFile are defined appropriately

pure writeToFile <*> readFile "input.txt"  -- Reads from "input.txt" and writes to "output.txt"

This example showcases the power of AFs in composing functions that operate within a context, in this case, the IO monad.

The Benefits of Embracing Functors and Applicative Functors

The use of fmap and AFs offers numerous benefits:

• Improved Code Readability: By abstracting away the details of the underlying data structure, the code becomes more concise and easier to understand.
• Enhanced Code Reusability: Functions using fmap and AFs can be applied to different data structures, promoting code reuse and reducing redundancy.
• Reduced Error Proneness: The inherent safety mechanisms within functors and applicative functors mitigate the risk of errors, leading to more reliable software.
• Enhanced Composability: The ability to chain and compose functions using fmap and AFs fosters a modular and flexible programming style.

Frequently Asked Questions

Q: What is the difference between fmap and applicative?

A: While both operate on functors, fmap applies a single function to the value within a functor, while applicative (<*>) allows applying functions that themselves operate on functors, enabling the composition of computations within a functorial context.

Q: Can I use fmap and applicative with any type?

A: Not all types are functors or applicative functors. A type must implement the necessary operations to qualify as a functor or an applicative functor.

Q: Why should I use functors and applicative functors?

A: They promote code clarity, reusability, and safety, ultimately leading to more maintainable and reliable software.

Q: Are there any limitations to using functors and applicative functors?

A: While powerful, they might not be the most efficient solution for all scenarios. For performance-critical applications, alternative approaches might be more suitable.

Tips for Effective Use of Functors and Applicative Functors

• Embrace the Abstraction: Focus on the operations you want to perform rather than the specific data structures involved.
• Chain Transformations: Use fmap to chain multiple transformations together, promoting code modularity and reusability.
• Leverage Applicative Functors for Complex Computations: Utilize AFs to compose functions that operate on functors, enabling sophisticated computations within a context.
• Explore Different Functor and Applicative Functor Instances: Familiarize yourself with the various instances available in your programming language, such as Maybe, List, IO, etc.

Conclusion

Functors and Applicative Functors, with their core concepts of fmap and the applicative function, offer a powerful paradigm for working with data structures and computations within a context. By leveraging these concepts, programmers can write code that is:

• Clear and Concise: Abstractions simplify code and make it easier to understand.
• Reusable and Modular: Functions can be applied across various data structures, promoting code reuse.
• Safe and Reliable: The inherent safety mechanisms within functors and applicative functors minimize the risk of errors.

While the initial learning curve might seem steep, embracing these concepts can lead to a more elegant, efficient, and maintainable approach to functional programming. As you delve deeper into the world of functors and applicative functors, you’ll discover their immense potential for crafting robust and expressive software solutions.

Closure

Thus, we hope this article has provided valuable insights into Navigating the Landscape of Functional Programming: A Comprehensive Exploration of fmap and Applicative Functors. We thank you for taking the time to read this article. See you in our next article!